1000x1000, 278.58 KB

1000x1000, 265.84 KB

1000x1000, 714.32 KB

1100x1100, 780.70 KB

1000x1000, 754.96 KB

1000x1000, 529.56 KB
| Home | Infos | Cubism | Cubism 2 | Stuff 1 | Kepler | Slicing | Spiral | Dice | Movies | unsorted |
A cube can be transformed by 24 differnt symmetry operations into itself (not taking into account the spatial inversion or mirror operations here). These symmetry operations are rotations about 90°, 180°, or 120°, depending on the symmetry axis and they constitute the cubic symmetry group 'O'.
Thus it is enough to take a 24th part of a cube (if this part has inversion symmetry) and to perform then the 24 different symmetry operations to get the full cubic object. As a cube has 6 faces, one can take one 4th of a face; or from the 12 edges, take 1/2 of one; or a 1/3 of one of the 8 corners - any of them transformed into the 24 equivalent positions gives a complete cubic symmetry.
The equation for the next row of images below is "plane01 * plane02 * ... * plane24 + k = 0", where "plane01 = x - 1 + 0.1*y + 0.1*z", i.e. a plane at "x = 1" with a slight tilting. The other planes are those obtained be the cubic symmetry operations.
If "k = 0", as in the first image, there is no coupling between the multiplicative parts (planes) of the equation. Nevertheless there are higher order singularities in the corners and because of numerical errors one sees a weak interaction there.
If "k ≠ 0", an interaction between the planes occurs at their intersection lines and some planes are bowing into others, whereas at the same time gaps open up. This can be seen in the next three pictures for "k = -0.0000001", "k = -0.00001", "k = -0.0001".

Off (100)-Planes, k = 0 1920x1200, 462.06 KB |

Off (100)-Planes, k=-0.0000001 1920x1200, 841.93 KB |

Off (100)-Planes, k=-0.00001 1920x1200, 999.14 KB |

Off (100)-Planes, k=-0.0001 1920x1200, 1.08 MB |
The images have pretty high resolution, like for a 24" wide screen monitor. Please scale down or cut out if they are too large for you. Under Windows I use the freeware IrfanView for image conversion, which is very convenient.
Below, some more images of the same type in the red color style. It should be mentioned that for the previous images, the additive constant k was always negative. This is also the case in the first image below, but for the 2nd image k is positive. This gives a different interaction of planes and the resulting space between the planes reveals a different cubic symmetry. Note, that eight spheres appeare here, just at the corners of a cube.
The third picture shows the mathematical product of intersecting cylinders which are slightly off the 111-directions (i.e. the cube diagonal) with an additive constant so that they couple with each other.
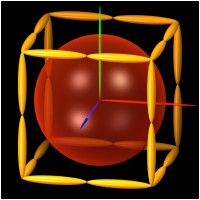
The last image in the row shows (100) planes at the faces of a cube. Due to 24 symmetry operations of the cube, several identical planes overlap and give quasi-singularities on the whole planes. This leads to troubles in the solution of the equations and gives the noisy planes. In addition, a unit sphere is shown.

Off (100)-Planes, k=-0.00001 1920x1200, 1016.92 KB |

Off (100)-Planes, k=+0.00001 1920x1200, 1.02 MB |

Off (111)-Cylinders 1920x1200, 818.67 KB |

(100)-Planes 1920x1200, 609.33 KB |
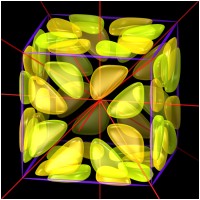
The next images explicitly present the full cubic symmetry group "O_h"

Triangular Elements 1000x1000, 465.54 KB |

Pyramidal Elements 1000x1000, 540.90 KB |
Pyramids, Rotation Axis 1000x1000, 606.65 KB |
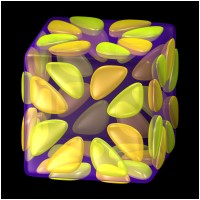
Pyramids on Cubic Surface 1000x1000, 506.66 KB |
If the surfaces elements are changed so that they are not limited, but open towards one side, a mixture of surfaces again with "O_h"-symmetry occurs.

Open Cubic Symmetry, clipped 1000x1000, 586.07 KB |

Open Cubic Symmetry 1000x1000, 750.86 KB |

Open Cub. Sym. 1400x1050 1400x1050, 987.48 KB |

Open Cub. Sym. 1920x1200 1920x1200, 1.30 MB |
| Home | Infos | Cubism | Stuff 1 | Kepler | Slicing | Spiral | Dice | Movies | unsorted |
e-mail: Gerhard.Brunthaler@jku.at