Conformal Mapping

Conformal mapping is a mathematical transformation, which preserves all crossing angles between lines. Here it is used to map the simple current flow in a square to more complex geometries in the plane. Under such a conformal mapping the electrical resistance of the area is the same before and after the transformation. I thank Thomas Hörmann to explore the theory behind it!

grid transformation and distortion due to conformal mapping
grid distortion
1800x1200, 300 KB
.
conformal mapping of current flow
conformal mapping
1500x1125, 834 KB
3000x2250, 2.6 MB
 conformal mapping of current flow with contact areas, poster
conformal mapping with contacts
1500x1125, 867 KB
3000x2250, 2.7 MB

In the images below, the red lines show the equipotential lines whereas the green paths represent the current flow. In the square the left and right hand borders are attached to metallic contacts so that the current flows parallel to upper and lower border from one side to the other. Without a magnetic field, the current flows parallel to the electric field and perpendicular to the equipotential lines, whereas with a magnetic field perpendicular to the plane, the electric current flow is deflected by an angle θH (the Hall angle) with respect to the electric field direction. The anlge between equipotential lines and current is than 90°-θH. For some images below, a Hall angle of θH = 45° is chosen.

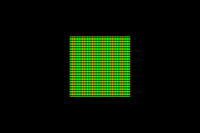
current flow in a square
square
1500x1000, 38 KB
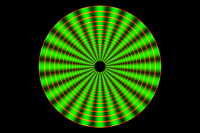
 conformal mapping of current flow to a ring
ring
1500x1000, 598 KB
 conformal mapping of current flow for two circles
two circles
1500x1000, 800 KB
current flow of a square in a magnetic field with Hall angle theta_H = 45°
parallelogram, theta_H = 45°
1500x1000, 94 KB
 conformal mapping of current flow to a ring in a magnetic field with Hall angle theta_H = 45°
ring, theta_H = 45°
1500x1000, 633 KB
 conformal mapping of current flow for two circles in a magnetic field with Hall angle theta_H = 45°
two circles, theta_H = 45°
1500x1000, 880 KB

Home

e-mail: Gerhard.Brunthaler(at)jku.at - replace (at) by @